√完了しました！ 立方体 求め 方 100038-立方体 体積 の 求め 方

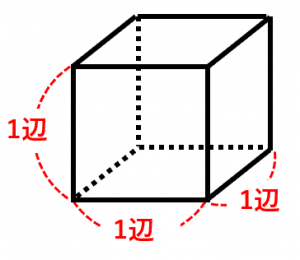
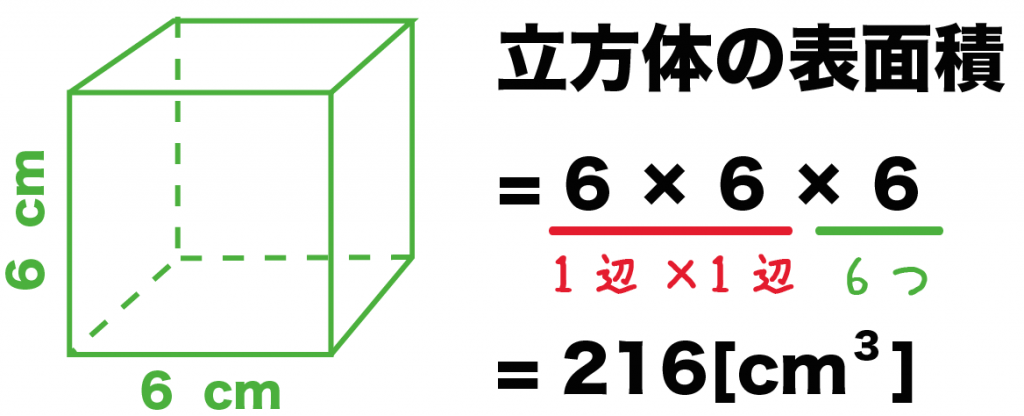
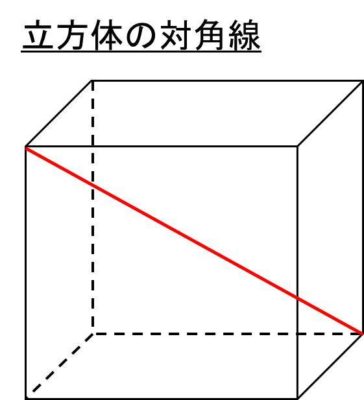
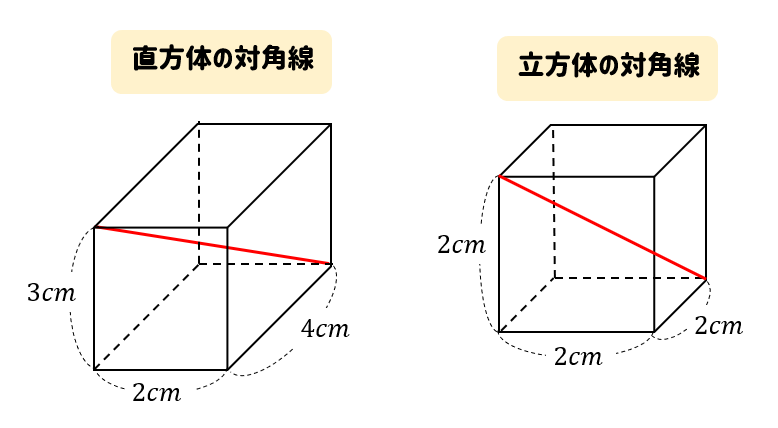
立方体の12の辺の長さは等しく、これを $a$ とします。立方体の表面積 $S$ は、次の式で求められます。 立方体の表面積 \begin{align*} V = 6a^2 \end{align*} 表面積 = 一辺 × 一辺 × 6 直方体や立方体の対角線の長さは、 2つの直角三角形に注目することで求めることができます。 ですが、公式を覚えておけば 計算の手間をかなり省けるのでおススメです！ なので、公式をしっかりと使いこなせるようにしておきましょう(/・ω・)/V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S 1 = 角錐底面積 S 2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体

公式を図解 すい体の体積 円すいの表面積の求め方

立方体 体積 の 求め 方

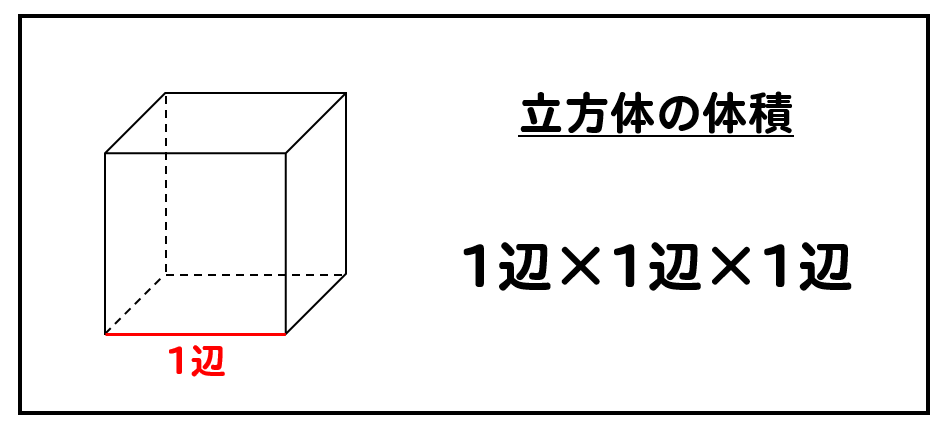
立方体 体積 の 求め 方- 立方体の体積の求め方には公式があるんだ。 立方体の1辺の長さをaとすると、その体積は、 aの三乗 で求めることができるよ。 つまり、立方体の体積は、 1辺×1辺×1辺 ってことになる。立方体の1辺の長さを3回かけてやればいいんだ。 これは立方体だから特別というわけじゃなくて、 ただ単に、 底面積×高さ「第499回 合否を分ける問題の解き方 立体図形の切断」 作図力が重要となる問題を、近年の中学入試の中から見てきています。 前回は「立体図形の影」をテーマにした問題について考えましたが、今回は「立体図形の切断」の問題を見ていきます。

四角錐台の体積 高精度計算サイト

 ・立体の体積を、直方体や立方体をもとにして、工夫して求めることができたことを振り返る。 ・求め方はいろいろあるが、答えは全て同じであることを押さえる。 活 か す 5．本時での学習事項を活かし、立体の体積を求める それが立方体というモノなのです。 なので、立方体も直方体の仲間ということになります。 だから、立方体も直方体の公式と同じく （たて）×（よこ）×（高さ） で求めることができます。 だけど、立方体の場合・第5学年で学習した直方体や立方体の求め方を基にして，四角 柱や三角柱の体積を求めるために，第5学年の教科書を振り返 る。 2 3 四角柱（直方体）の体積の 求め方を「底面積×高さ」と 見直し，底面が直角三角形の 三角柱の体積の求め方も同様

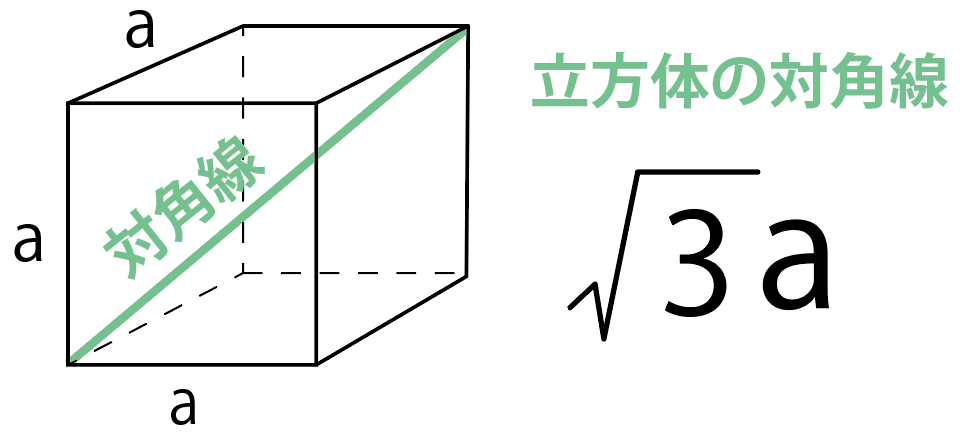
立方体の対角線の長さは、 立方体の辺の長さに $\sqrt{3}$ をかける と求められます。 なので、例えば、辺の長さが $a$ の立方体の場合には、 対角線の長さは、 対角線の長さ $=$ 辺の長さ $\times\sqrt{3}$ $=a\times\sqrt{3}$ $=\sqrt{3}\, a$よねさんのExcelとWordの使い方 » ワード10基本講座 » 図や図形・クリップアート » 図形の3D効果 ワード10基本講座：図形の3D効果 ワード10では図形の「3D効果」がリボンからなくなった小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 小学5年生の算数 体積 直方体と立方体の体積の求め方 練習プリント;

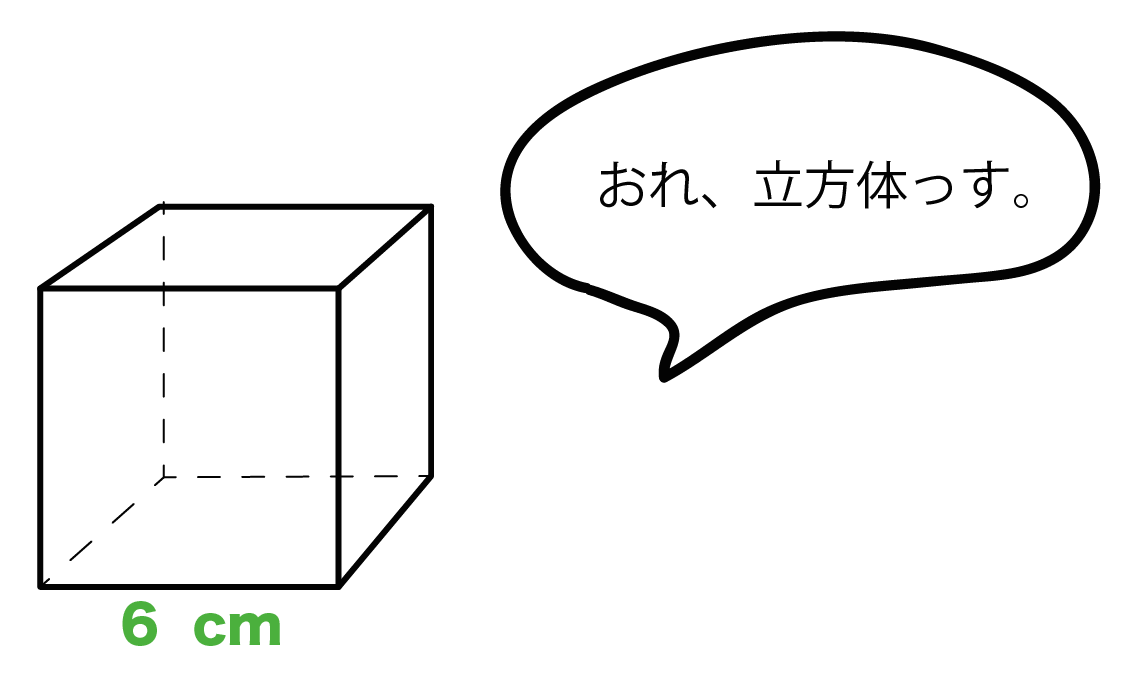
立方体の場合、縦・横・高さがすべて一辺の長さとなるので、体積は 『1辺×1辺×1辺』 と表せます。 たとえば以下のような問題の場合。 例題 「一辺 4cm 4 c m の立方体」と「縦 3cm 3 c m ・横 4cm 4 c m ・高さ 5cm 5 c m の直方体」の体積をそれぞれ求めよ。 それぞれの面積はこのように計算できます。 立方体の体積： 4× 4×4＝64(cm3) 4 × 4 × 4 ＝ 64 ( c m 3) 直方体の体積： 3× 立方体の体積の計算問題を解いてみよう それでは、立方体の体積の求め方に慣れるためにも計算問題を解いていきましょう。 ・例題3 1辺の長さが2cmの立方体の体積はいくらでしょうか。 ・解答3 上の立方体の体積の公式を元に計算していきます。立体は円柱になり，表面積は底面積×2=16 π ×2 (cm 2 )と側面積8 π ×7 (cm 2 )の合計になります 底面積2つで32 π (cm 2 )，側面積56 π (cm 2 )の合計は π (cm 2 ) (答) ※以下，8番以後の問題を解くには，中学校3年生で習う三平方の定理が必要になります．まだ習っ

立方体の表面積を求める計算と公式 辺と表面積の対応表つき Irohabook

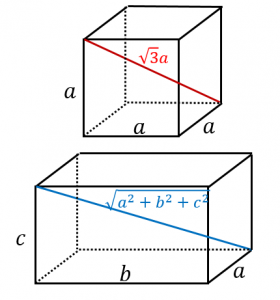
立方体と直方体の対角線の長さ 具体例で学ぶ数学

  立方体や直方体の体積の求め方を習ったら、少し応用的な問題にも取り組みましょう。展開図を見て、体積を求める問題や、いくつかの立方体や直方体の面積を足したり引いたりして解く問題です。 直方体の体積を求め直方体と立方体の体積の求め方を考えます。 1辺が 1 cm の立方体が何個分あるかで求めることができます。 縦×横×高さ＝直方体の体積，1辺×1辺×1辺＝立方体の体積となります。 立体の体積の求め方（公式）を一覧にまとめました。 公式を忘れてしまったときには、こちらで確認しましょう。 体積の求め方公式 立方体・直方体の体積の求め方 円柱の体積の求め方 三角柱の体積の求め方 円錐の体積の求め方 四角錐の体積の求め方 注意 スポンサードリンク (adsbygoogle

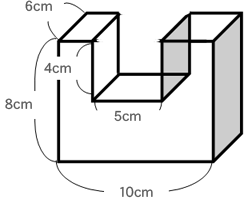
体積 直方体と立方体のかさを表そう 第５学年 小学校 算数 My実践事例 日本文教出版

面積や体積のかけ算の順序 おかしな算数教育 身勝手な主張

 錐の体積の公式の求め方 ① 立方体を用意する。 そのまんまです。1辺がaの立方体を書いてみましょう。 1辺がaなので、この立方体の体積は、 a×a×a＝a 3 ですね。 下の図をイメージしてください。 ② 中心に点を打つ。2 dagar sedan 空間図形 角柱・角錐(すい)・円柱・円錐の体積の求め方 空間図形 ねじれの位置とは？ 空間図形 辺や面を表すときのアルファベット順 空間図形 母線とは何か 空間図形 立方体を切断したときの切り口の考え方この立方体を4点 m, e, g, n を通る平面で2つの立体に切る。 このとき，次の(1)～(5)の各問いに答えなさい。 (4) 2つの立体のうち，頂点 B を含む立体の体積を求めよ。

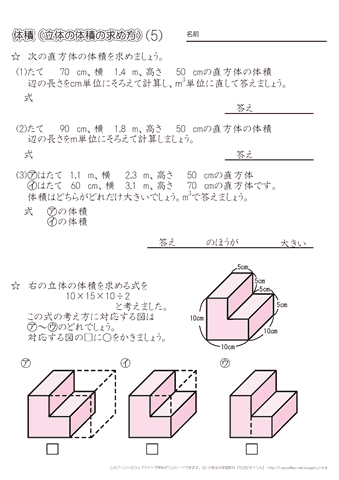
小学５年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生

立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 小学校 算数 学習

 ってことさ。 たとえば、下の辺が4cm、上の辺が2 cm、高さ6cmの正四角錐台ABCDEFGHがあったとしよう。 この立体の体積は、 1/3 h ( a^2 ab b^2 ) = 1/3 × 6 × ( 4^2 4 × 2 2^2) = 2 × ( 16 8 4 ) = 56 cm^3 になるよ！ めんどい計算式だけど、Course Summary 小学5年生 直方体と立方体の体積、体積の求め方のくふう、高さと体積の関係、いろいろな体積の単位 みなさん、初めまして。 本講座を担当している葉一（はいち）と申します。 私は元塾講師なのですが、塾講師として勤務していた期間 今回は練習ということで、\(cm^3\)と\(m^3\)の両方の場合を求めます。 ↑ 4 この時は立方体なので一辺を3回と考えてもOKです。ただ、体積を求めるときは立方体を特に意識しなくても直方体の体積の求め方だけを意識させておけば大丈夫です。

直方体 立方体の体積 Youtube

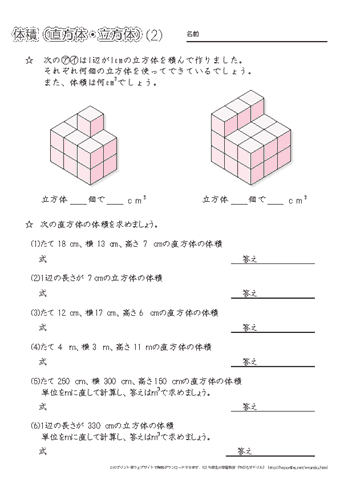
小学５年生の算数 体積 直方体と立方体の体積の求め方 練習プリント ちびむすドリル 小学生

立方体の体積 下図が立方体です。立方体は全ての辺が同じ長さなので、体積の計算も簡単です。縦×横×高さを計算すれば良いですね。 よって、 立方体の体積＝4×4×4＝64cm 3 です。 立方体の体積は？1分でわかる計算、単位、公式、求め方、リットルとの関係求める体積は ＝352cm 3 。 表面積 直方体2本の表面積は （4×4×212×4×4）×2 ＝448cm 2 。 重なっている表面積は 4×4×22×4×4＝64cm 2 。 求める表面積は＝384cm 2 。方を基に，四角柱の進んで調べようとの求め方を，直 体積の求め方を考えしている。 方体の体積の求 る。 め方から類推し て考えている。 2・角柱の体積の求め方 角柱の体積を， を考え，角柱の体積 公式を用いて求め を｢底面積×高さ｣の ることができる。

立方体の体積 小学生はどうやって問題解く 計算のやり方を解説 数スタ

円柱の表面積の求め方 立方体 円錐の投影図 中学１年数学 空間図形

地図の体積計測

立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式

一辺が12cmの立方体の中にある三角錐の体積の求め方を教えてく Yahoo 知恵袋

体積の求め方 計算公式一覧

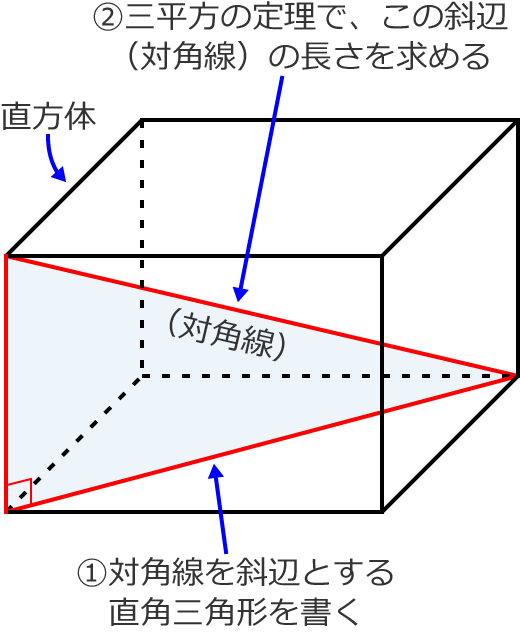
直方体の対角線の長さの求め方

三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学

立方体 直方体の体積の求め方 公式 小学生 中学生の勉強

兵庫県実践事例 算数小学校６年

私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館

立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式

体積の求め方 計算公式一覧

公式を図解 すい体の体積 円すいの表面積の求め方

立方体 直方体の体積の求め方 公式 小学生 中学生の勉強

計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく

立方体 直方体の体積の求め方 公式 小学生 中学生の勉強

三角錐の体積の求め方 下の図は立方体から三角錐を切り取った立 Yahoo 知恵袋

小5算数 直方体や立方体の体積の求め方がわかるかな Youtube

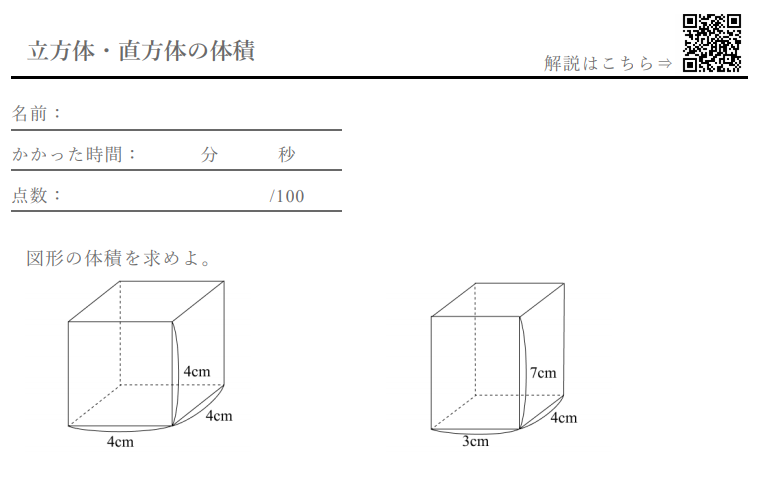
立方体 直方体 の体積 計算ドリル 問題集 数学fun

5年 直方体と立方体の体積 算数イメージ動画集 大日本図書

５年算数体積２わかる教え方

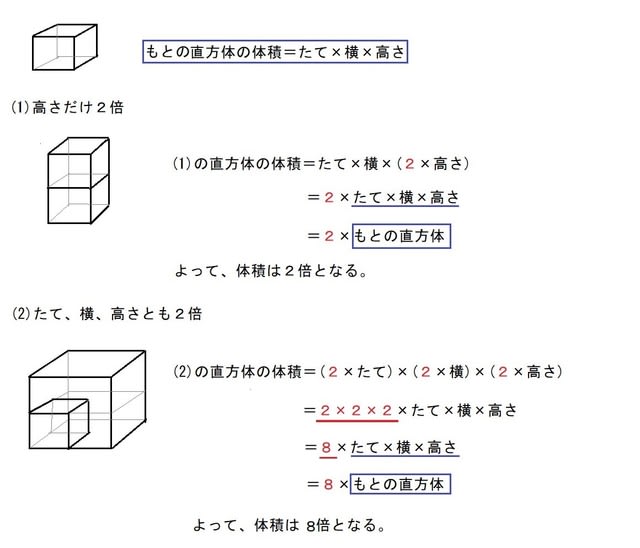
直方体 立方体の体積 小５ きちんと式を書けば簡単 算数の教え方教えますmother S Math Happy Study Support

立方体 りっぽうたい とは何 Weblio辞書

マスラボ 小学校5年 体積 レベル3 立方体の体積の求め方 Youtube

三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学

Www Nagoya C Ed Jp School Shimizu E 5sansu A Pdf

体積の測定 測定のことを 即 知りたい ソクシリ キーエンス

立方体の中の四角錐の底面積の求め方教えてください Clear

密度の計算と求め方 勉強のポイントは公式の理解と変換

算数 積み上げた立方体の個数 なるほどの素

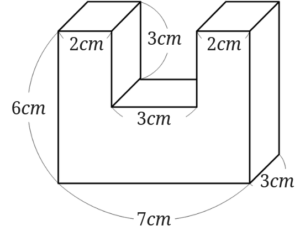
直方体や立方体の体積を求める応用問題の解き方は どうやって教えるといいの みけねこ小学校

1

直方体や立方体の体積を求める公式は どうして たて 横 高さ なの みけねこ小学校

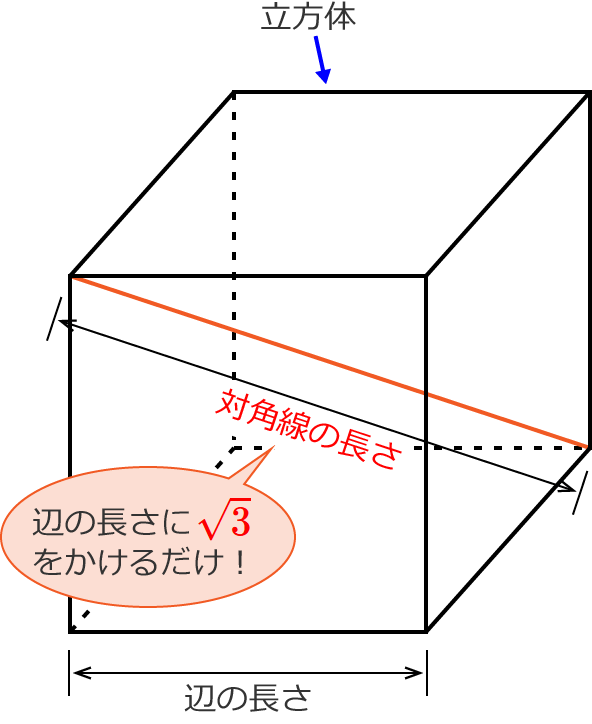
立方体の対角線の長さの求め方

立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式

3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ

算数科予習プリント 体積の求め方は考えられたかな 翁島 おきなしま 小学校ホームページ

中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー

体積の求め方 計算公式一覧

計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく

Math 積み重ねた立方体の表面積 働きアリ

小５ 算数 小５ ５ 体積の求め方のくふう Youtube

どうして1 3なの 錐の体積の公式の求め方 まなべーと

立方体の中の四角錐の底面積の求め方教えてください Clear

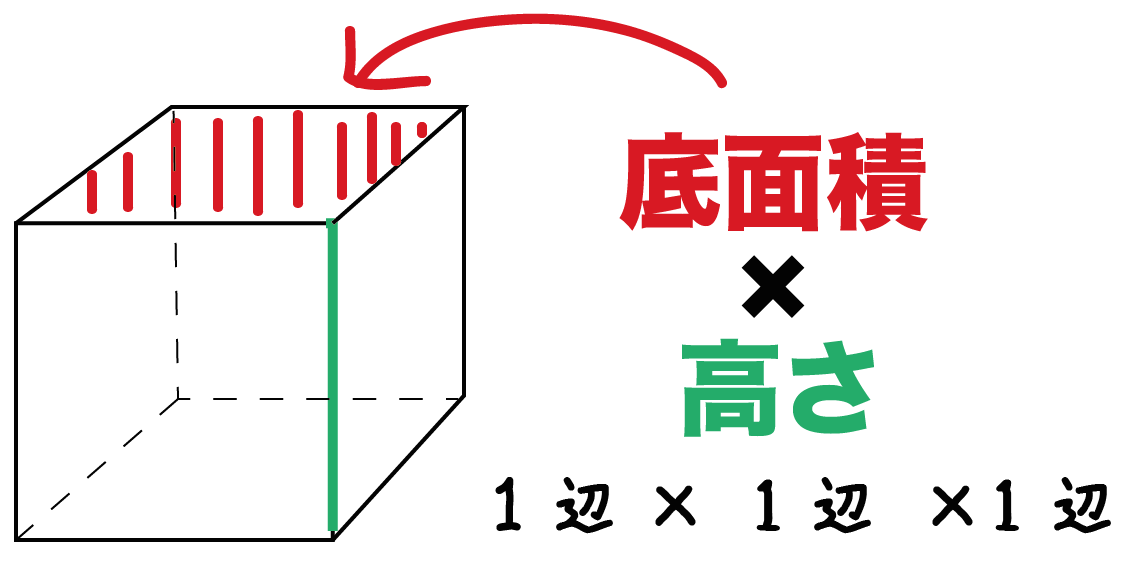
計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく

立方体と直方体の体積を計算する方法とツール 具体例で学ぶ数学

計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく

計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく

小5 複雑な立体の体積 直方体 日本語版 Youtube

Http Www Shunan Ed Jp Tokuyamasho 6nensannsuurittai Pdf

５年算数体積２わかる教え方

５年算数体積２わかる教え方

四角錐台の体積 高精度計算サイト

直方体を組み合わせた立方体の面積 写真参照 を解きたいのですが Yahoo 知恵袋

複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座

算数流体積の求め方 Sciencelab 冨田塾

計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく

1

立方体の表面積の求め方は 1分でわかる計算 公式 直方体の表面積の求め方

直方体と立方体の体積 算数 数学が好きになりmath

立方体の対角線の計算方法 白丸くん

すきるまドリル 小学５年生 算数 体積 無料学習プリント すきるまドリル 無料学習プリント

直方体 立方体の対角線の長さは公式でラクラク計算できるぞ 数スタ

立方体 直方体の体積の求め方 公式 小学生 中学生の勉強

小学5年生の算数 動画 体積の求め方のくふうの問題 19ch

立方体の表面積の求め方は 1分でわかる計算 公式 直方体の表面積の求め方

立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム

容積の求め方 小学生の算数質問ひろば 進研ゼミ小学講座

立方体の辺の求め方を教えてください 容積が分かっていて1辺の長 Yahoo 知恵袋

1

計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく

計算公式 立方体の対角線の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

体積の求め方 計算公式一覧

体積の応用

体積 上 体積の意味から 立方体 直方体 柱 錐の体積の求め方 思考力算数練習張シリーズ 46 エム アクセス 本 通販 Amazon

三角錐 四面体 の体積の公式 Schoolmath S Diary

計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく

1

小学５年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生

中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット

小学算数 立体の体積の公式と単位 立方体 直方体 円柱 三角柱 偏差値40プログラマー

立方体の体積は 1分でわかる計算 単位 公式 求め方 リットルとの関係

Math 積み重ねた立方体の表面積 働きアリ

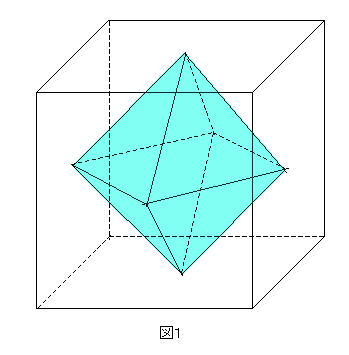
空間図形 練習問題 9 ネット塾

中1理科 密度の計算のコツ 映像授業のtry It トライイット

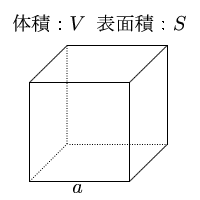
立方体の体積から1辺 体積 表面積の計算 計算サイト

５年算数体積２わかる教え方

計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく

小５ 算数 小５ ３ 直方体と立方体の体積 Youtube

小学6年生の問題です Aからfの点はそれぞれ立方体の面の対角線の交点です Yahoo 知恵袋

６年算数立体の体積１ 教え方

立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun

立方体 直方体の体積の求め方 公式 小学生 中学生の勉強

授業 直方体と立方体 １ 算数 小４ 群馬県 Youtube

小学５年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生

Incoming Term: 立方体 体積 の 求め 方,